1 引言
Bergen和Hill首先提出了網(wǎng)絡(luò)結(jié)構(gòu)保持模型[1](Network Structure Preserving Model),隨后文[2]、[3]又分別在此基礎(chǔ)上做了改進(jìn)。由于建模考慮了網(wǎng)絡(luò)結(jié)構(gòu),涉及到負(fù)荷節(jié)點(diǎn),使得模型中引入了潮流約束方程。 這樣,結(jié)構(gòu)保持模型被表示成一組微分代數(shù)方程DAE。該模型雖然能更加準(zhǔn)確地描述電力系統(tǒng),但將傳統(tǒng)的穩(wěn)定性判定方法應(yīng)用于其上時(shí)卻出現(xiàn)了較大的困難。
將傳統(tǒng)Controlling UEP推廣至結(jié)構(gòu)保持模型,除EEAC方法[4]本身所具有的特點(diǎn)使其不受DAE影響之外,文[5]~[13]分別利用局部分析方法及奇異攝動方法還做出了許多卓有成效的工作。其中,局部分析方法雖然理論上很完備,但由于奇異面的存在而不能獲得全局的結(jié)論,而且每個(gè)代數(shù)子流形都對應(yīng)于不同的ODE,使得它難以應(yīng)用。奇異攝動方法,即所謂的邊界層方程BLE,通過它可得到對應(yīng)于DAE的BLE。在某些范圍內(nèi),BLE可以近似地表示DAE的動態(tài)特性,而且對基于BLE的電力系統(tǒng)模型運(yùn)用Controlling UEP方法能夠保證持續(xù)故障軌跡與故障后系統(tǒng)穩(wěn)定域邊界相撞。雖然將DAE轉(zhuǎn)化為BLE可以獲得全局結(jié)論,但這并沒有得到證明,況且并非任何情況下DAE都可以等價(jià)的轉(zhuǎn)化為BLE。
由上可見,Controlling UEP應(yīng)用于結(jié)構(gòu)保持模型較經(jīng)典模型要困難得多,而且準(zhǔn)確的負(fù)荷建模一直是個(gè)難題[14]。文[15]的理論分析部分已經(jīng)討論了結(jié)構(gòu)保持模型中的奇異性質(zhì)以及傳統(tǒng)Controlling UEP理論應(yīng)用于該模型的難點(diǎn),并就此對外部跳變行為和故障后DAE系統(tǒng)的穩(wěn)定性進(jìn)行了分析。在此基礎(chǔ)上,本文將提出基于結(jié)構(gòu)保持模型的穩(wěn)定性判定方法。
2 現(xiàn)有方法概述及問題
由于代數(shù)流形的約束、跳變行為的存在等原因,使得傳統(tǒng)的直接法難以應(yīng)用于結(jié)構(gòu)保持模型中。文[5]~[13]從兩方面提出了解決方法,其分別是應(yīng)用隱函數(shù)定理將DAE在代數(shù)流形上等價(jià)轉(zhuǎn)化為ODE,本文稱之為局部分析方法;另一種是應(yīng)用奇異攝動方法,將DAE轉(zhuǎn)化為BLE,本文稱之為奇異攝動方法。這兩種方法的共同目標(biāo)是相同的,即將DAE化為傳統(tǒng)的Controlling UEP能夠應(yīng)用的一組常微分方程。但它們分別存在各自的缺點(diǎn)。
對于局部分析方法,主要存在以下問題:
(1) 不能提出全局的結(jié)論[5,16];
(2) 沒有考慮外部跳變行為。
雖然存在以上問題,但局部分析方法在確定代數(shù)子流形上是準(zhǔn)確的,理論上也是完備的。
S. Sastry等[12,17]首先將奇異攝動方法引入結(jié)構(gòu)保持模型,隨后[7,9~11,13]都在該方面做了深入的研究。對于奇異攝動方法,主要存在以下問題:
(1)DAE不能在任何情況下都等價(jià)地轉(zhuǎn)化為BLE。
(2)攝動參數(shù)e 的符號確定。同樣的e?0,但e <0和e <0對應(yīng)的BLE軌跡完全不同。文中符號選擇的原則是保證BLE與原DAE系統(tǒng)對應(yīng)的平衡點(diǎn)具有相同穩(wěn)定屬性。
(3)對于相同的持續(xù)故障軌跡,不同的e可能使Controlling UEP不同。那么當(dāng)e?0時(shí),Controlling UEP是否趨于同一個(gè)。
文[7]、[9]建議通過奇異攝動方法將DAE系統(tǒng)和能量函數(shù)方法聯(lián)系起來,從而獲得一個(gè)全局的結(jié)論。而且BLE存在與e >0無關(guān)的能量函數(shù)容易構(gòu)造[7,9]。但因BLE系統(tǒng)并不和DAE系統(tǒng)等價(jià),它們的軌跡在某些時(shí)候也不盡相同,現(xiàn)有判定方法的獲得仍需通過啟發(fā)式的推導(dǎo)。
3 擴(kuò)展Controlling UEP(ECUEP)方法
3.1 方法提出
為了克服上述方法存在的問題并結(jié)合它們的優(yōu)點(diǎn), 本節(jié)將在文[15]中定理3的基礎(chǔ)上提出新的暫態(tài)穩(wěn)定判定方法,并給出仿真算例。
定義1 BLE系統(tǒng)是以O(shè)DE形式表示的,給定e >0, 通過持續(xù)故障軌跡Ff(t) 都能唯一地得到Controlling UEP,記為 為方便起見,將其稱作Ff(t)的e-Controlling UEP。
為方便起見,將其稱作Ff(t)的e-Controlling UEP。
引理1 Ff(t)為給定的持續(xù)故障軌跡,初值Ff(tf)?D0。當(dāng)故障持續(xù)發(fā)展時(shí),則存在:

定義2 Ff(t)為持續(xù)故障軌跡,初值Ff(tf)?D0。若存在序列ek?0+,使Ff(t)主導(dǎo)的e-Controlling UEP都對應(yīng)于同一個(gè)UEP,則稱該UEP為不變Controlling UEP。

引理2 Ff(t)為持續(xù)故障軌跡,初值Ff(tf) ?D0。若BLE的穩(wěn)定域是局部嚴(yán)格等度連續(xù),則不變Controlling UEP是唯一的。
證明:由定義2及定義3可直接推出該引理。

其證明參見附錄B。


其證明見附錄C。
雖然本文的討論未涉及奇異面,但奇異面對暫態(tài)過程的影響是非常重要和復(fù)雜的[5,6,16]。上述定理對暫態(tài)過程中由奇異面主導(dǎo)的電壓失穩(wěn)不能做出判定,因此, 為排除實(shí)際判定中奇異面的影響,可以通過計(jì)算代數(shù)方程雅克比矩陣的條件數(shù)方法來判定系統(tǒng)軌跡是否靠近奇異面,或運(yùn)用文[16]提出的勢能方法(Potential Energy bbbbbb)。下面,給出基于結(jié)構(gòu)保持模型的ECUEP方法。
擴(kuò)展Controlling UEP方法(ECUEP):設(shè)BLE系統(tǒng)的穩(wěn)定域是局部嚴(yán)格等度連續(xù)的。
(1)臨界能量的確定步驟

DAE系統(tǒng)的能量函數(shù)EDAE(·)一般很難構(gòu)造。因此在這里,它可以由能量函數(shù)E(·)作合理的替代。
(2)穩(wěn)定性判定步驟
1)使用給定的持續(xù)故障軌跡和虛擬持續(xù)故障跳變軌跡, 計(jì)算故障清除時(shí)刻的能量函數(shù)值E(·)、EDAE(·)。

3.2 仿真算例
考慮如圖1所示的單機(jī)-兩母線系統(tǒng)[18]。系統(tǒng)的DAE模型如式(3)所示。其中,p3=2,q3=1。由于系統(tǒng)較為簡單,由式(3)可以求得系統(tǒng)SEP附近的代數(shù)流形、UEP及死巷點(diǎn)(這些是本文所關(guān)心的),見圖2。
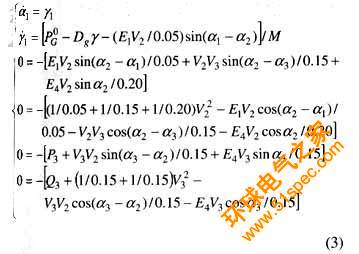

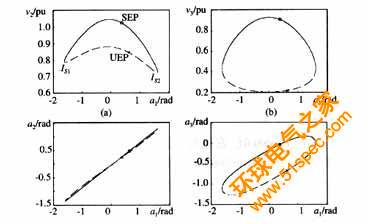

例1 對圖1所示系統(tǒng),考慮母線B2三相短路故障,且故障后系統(tǒng)與原系統(tǒng)保持一致。對于給定的故障及實(shí)際故障軌跡末值,根據(jù)ECUEP方法,判斷系統(tǒng)的暫態(tài)穩(wěn)定性步驟如下:
(1)求取對應(yīng)于BLE系統(tǒng)及DAE系統(tǒng)的Controlling UEP
1) 求取BLE系統(tǒng)的Controlling UEP。
求取Controlling UEP一直是相關(guān)不穩(wěn)定平衡點(diǎn)方法應(yīng)用的障礙,BCU方法[7,19]的提出使得這一問題得以較快速準(zhǔn)確地解決。本文運(yùn)用BCU方法解得BLE系統(tǒng)的Controlling UEP為(0.6279,0.4659,0.8454, -0.6786,0.2147)
注1 運(yùn)用文[7]給出的概念性結(jié)構(gòu)保持BCU方法(Conceptual Network-Preserving BCU bbbbbb)及文[19]給出的方法計(jì)算Controlling UEP,當(dāng)給定的e 很小時(shí),BLE系統(tǒng)在數(shù)值上具有較強(qiáng)的病態(tài)特性,由持續(xù)故障軌跡從系統(tǒng)穩(wěn)定域邊界上的逸出點(diǎn)作為初值對故障后的降維系統(tǒng)進(jìn)行積分,所得到的降維系統(tǒng)軌跡迅速趨于Lh附近,只有很弱的靠近Controlling UEP的趨勢,如圖3。如果將e 取大些,則故障后降維系統(tǒng)的軌跡在某一時(shí)刻較為趨于某UEP,如圖4。而且隨著e的增大,趨近程度越來越大,這樣根據(jù)文[7]、[19]給出的方法,可以順利地求出Controlling UEP,但是也不能將e 取得過大。所以BLE系統(tǒng)中求取Controlling UEP仍是非常困難的。不過,一些特殊的算法,如DASSL[20]可能會對此有所幫助,但仍需進(jìn)一步研究。

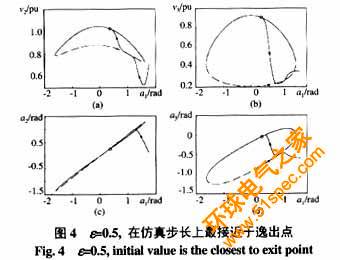
2)求取DAE系統(tǒng)的Controlling UEP。
盡管在Lh沒有UEP,但是Lh邊界是死巷點(diǎn)。故障后軌跡撞到死巷點(diǎn)仍然是危險(xiǎn)的,運(yùn)用文[16]提出的勢能方法,用相關(guān)死巷點(diǎn)IS的能量函數(shù)值替代Controlling UEP,來作為DAE系統(tǒng)暫態(tài)穩(wěn)定判定的臨界能量。根據(jù)虛擬持續(xù)故障跳變軌跡可得相關(guān)的死巷點(diǎn)為(1.636,1.282,0.724, 0.003,0.433)。
(2)求取臨界能量函數(shù)值
應(yīng)用文[5],[16],[18],[21]定義的能量函數(shù)

 則求取臨界能量函數(shù)值的步驟為:
則求取臨界能量函數(shù)值的步驟為:
1)求取故障切除點(diǎn)及其對應(yīng)虛擬跳躍點(diǎn)的能量函數(shù)值實(shí)際故障軌跡末值為p=(1.15,0.48,0.29,0.81, -0.33,0.53),其對應(yīng)的外部跳變目標(biāo)點(diǎn)為q=(1.15,0.48,0.84,0.89,0.15,0.74),則E(p)=11.4710,E(q)=8.9735。
2)分別比較能量函數(shù)值
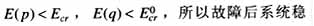 定,如圖5、6所示。
定,如圖5、6所示。


例2 對圖1所示系統(tǒng),考慮母線B2發(fā)生短路故障,且故障后系統(tǒng)與原系統(tǒng)保持一致。對于給定故障及實(shí)際故障軌跡末值,根據(jù)ECUEP方法,判斷系統(tǒng)的暫態(tài)穩(wěn)定性。
其步驟如下:
(1)同例1的步驟(1)。
(2)該步驟分兩步,
1)實(shí)際故障軌跡末值為p=(1.48,0.56, 0.30,0.61, -0.40,0.37),其對應(yīng)的外部跳變目標(biāo)點(diǎn)為q=(1.48,0.56,1.12,0.79,,0.14,0.59),則E(q)= 14.8441,E(p)= 24.6886;
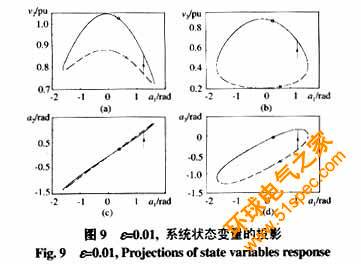
2)  但E(P)>Ecr,所以故障后系統(tǒng)不穩(wěn)定,如圖7、8所示。故障后軌跡趨于一不可運(yùn)行的穩(wěn)定平衡點(diǎn)(0.628,0,0.466,0.845,-3.820, -0.215)。
但E(P)>Ecr,所以故障后系統(tǒng)不穩(wěn)定,如圖7、8所示。故障后軌跡趨于一不可運(yùn)行的穩(wěn)定平衡點(diǎn)(0.628,0,0.466,0.845,-3.820, -0.215)。


注2 由圖7
4 ECUEP方法的改進(jìn)
針對例1和例2,使用ECUEP方法及文[7]給出的概念性結(jié)構(gòu)保持BCU方法分別進(jìn)行暫態(tài)穩(wěn)定分析,判定過程和結(jié)果比較如表1。
由表1可見,就本章給出的例子,文[7]給出的BCU方法能夠與ECUEP方法獲得相同的判定結(jié)果,但計(jì)算量卻減少一半。而且,由于Controlling UEP方法的保守性,使用它在進(jìn)行外部跳變判定時(shí)常常出現(xiàn)保守的誤判。可知,故障后軌跡沒有降落到Lh上,系統(tǒng)不穩(wěn)定。而僅根據(jù)虛擬跳躍目標(biāo)點(diǎn)判定,故障后系統(tǒng)應(yīng)該是穩(wěn)定的。從圖中可以看出,對外部跳躍的方向作出判斷是必要的。否則,僅考慮DAE系統(tǒng)的子模式x=f[x,h(x)]會引起故障后系統(tǒng)穩(wěn)定性的誤判。

根據(jù)文[15]中的定義2,BLE軌跡會在很短時(shí)間內(nèi)逼近DAE的某一代數(shù)子流形,那么通過數(shù)值仿真,可以僅對BLE系統(tǒng)計(jì)算若干個(gè)步長便能夠得到外部跳變方向及降落的代數(shù)子流形。如果假定仿真中不存在數(shù)值問題,那么,運(yùn)用數(shù)值仿真的方法來判定外部跳變不僅可以克服Controlling UEP方法的保守性,而且也可以迅速地獲得結(jié)果。對BLE系統(tǒng)的仿真目的在于:判定外部跳變行為時(shí),只需仿真至能夠獲得結(jié)果便可停止,所以它與以前所說的用時(shí)域仿真方法來判定暫態(tài)穩(wěn)定性是有區(qū)別的。
綜上所述,對ECUEP方法進(jìn)行改進(jìn),可引入數(shù)值計(jì)算方法來判定外部跳變行為。將改進(jìn)后的ECUEP方法稱為混合ECUEP方法(Hybrid ECUEP bbbbbb),其步驟如下:
(1)外部跳變行為的確定
以p為初值,對故障后DAE系統(tǒng)所對應(yīng)的BLE系統(tǒng)進(jìn)行數(shù)值仿真,并根據(jù)BLE軌跡來判定故障后系統(tǒng)是否外部跳變至Lh。如果跳變至Lh,則需要步驟2和3的進(jìn)一步判定;如果不跳變至Lh,則判定故障后系統(tǒng)不穩(wěn)定。
(2)臨界能量的確定
1)由持續(xù)故障軌跡對應(yīng)的虛擬持續(xù)故障跳變軌跡,找到DAE的Controlling UEPp0,co;
 (3)穩(wěn)定性判定
(3)穩(wěn)定性判定
 例3 對圖1所示系統(tǒng),考慮母線B2三相短路故障,且故障后系統(tǒng)與原系統(tǒng)保持一致。對于給定故障及實(shí)際故障軌跡末值,根據(jù)Hybrid ECUEP、ECUEP和文[7]給出的BCU方法,分別判斷系統(tǒng)的暫態(tài)穩(wěn)定性。
例3 對圖1所示系統(tǒng),考慮母線B2三相短路故障,且故障后系統(tǒng)與原系統(tǒng)保持一致。對于給定故障及實(shí)際故障軌跡末值,根據(jù)Hybrid ECUEP、ECUEP和文[7]給出的BCU方法,分別判斷系統(tǒng)的暫態(tài)穩(wěn)定性。
首先,使用Hybrid ECUEP方法進(jìn)行暫態(tài)穩(wěn)定判定。其步驟為:
(1) p=(1.25,0.50,0.29,0.75,-0.35,0.50),計(jì)算得到跳變降落代數(shù)子流形為Lh;
(2)此例使用與例1相同的系統(tǒng),只是增大故障的持續(xù)時(shí)間,所以根據(jù)例1可知, 18.1323;
18.1323;


例4:
(1)同例1步驟(1)。
(2) p=(1.25,0.50,0.29,0.75,-0.35,0.50),其對應(yīng)的外部跳變目標(biāo)點(diǎn)為q=(1.25,0.50,0.92,0.86,0.16,0.70),則E(q)=10.6447,E(p)=18.5751。
(3)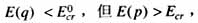 所以使用ECUEP方法及文[7]給出的BCU方法都判定故障后系統(tǒng)不穩(wěn)定。
所以使用ECUEP方法及文[7]給出的BCU方法都判定故障后系統(tǒng)不穩(wěn)定。
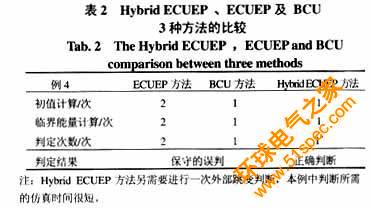
針對例3,分別使用Hybrid ECUEP方法、ECUEP方法及文[7]給出的概念性結(jié)構(gòu)保持BCU方法進(jìn)行暫態(tài)穩(wěn)定分析,分析結(jié)果見表2。由表2可見,對例3而言,ECUEP方法和文[7]給出的BCU方法得出了保守的誤判,Hybrid ECUEP方法判定正確。與ECUEP方法相比,Hybrid ECUEP方法不僅改善了保守性,而且判定過程得到簡化;與文[7]給出的BCU方法相比,Hybrid ECUEP方法有限地增加了判定時(shí)間,但可以換來更加準(zhǔn)確的判定。使用ECUEP方法及文[7]給出的BCU方法進(jìn)行暫態(tài)穩(wěn)定判定。此例使用的系統(tǒng)與例1相同,僅增大故障的持續(xù)時(shí)間,其步驟為
5 結(jié)論
本文概述了現(xiàn)有基于結(jié)構(gòu)保持模型的判定方法及存在的問題。在結(jié)合兩者優(yōu)點(diǎn)及文[16]定理3的基礎(chǔ)上,提出了新的穩(wěn)定性判定方法,并給出了具體算例,得出如下結(jié)論:
(1)以傳統(tǒng)Controlling UEP方法為依托,結(jié)合現(xiàn)有兩種分析方法的優(yōu)點(diǎn),在對外部跳變行為討論的基礎(chǔ)上,提出新的基于結(jié)構(gòu)保持模型的暫態(tài)穩(wěn)定分析直接法——擴(kuò)展Controlling UEP方法。
(2)在ECUEP方法的基礎(chǔ)上,以數(shù)值仿真來替代一部分能量函數(shù)的比較,提出Hybrid ECUEP方法,從而提高了判定的實(shí)用性與準(zhǔn)確性。
附錄A:引理1的證明

附錄B 定理1的證明



附錄C 定理2的證明


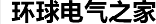








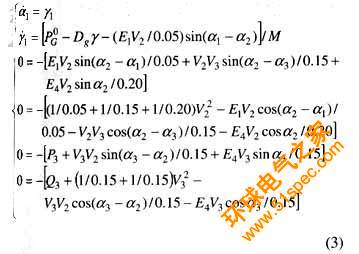






 則求取臨界能量函數(shù)值的步驟為:
則求取臨界能量函數(shù)值的步驟為: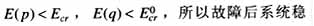 定,如圖5、6所示。
定,如圖5、6所示。

 但E(P)>Ecr,所以故障后系統(tǒng)不穩(wěn)定,如圖7、8所示。故障后軌跡趨于一不可運(yùn)行的穩(wěn)定平衡點(diǎn)(0.628,0,0.466,0.845,-3.820, -0.215)。
但E(P)>Ecr,所以故障后系統(tǒng)不穩(wěn)定,如圖7、8所示。故障后軌跡趨于一不可運(yùn)行的穩(wěn)定平衡點(diǎn)(0.628,0,0.466,0.845,-3.820, -0.215)。

 (3)穩(wěn)定性判定
(3)穩(wěn)定性判定 例3 對圖1所示系統(tǒng),考慮母線B2三相短路故障,且故障后系統(tǒng)與原系統(tǒng)保持一致。對于給定故障及實(shí)際故障軌跡末值,根據(jù)Hybrid ECUEP、ECUEP和文[7]給出的BCU方法,分別判斷系統(tǒng)的暫態(tài)穩(wěn)定性。
例3 對圖1所示系統(tǒng),考慮母線B2三相短路故障,且故障后系統(tǒng)與原系統(tǒng)保持一致。對于給定故障及實(shí)際故障軌跡末值,根據(jù)Hybrid ECUEP、ECUEP和文[7]給出的BCU方法,分別判斷系統(tǒng)的暫態(tài)穩(wěn)定性。 18.1323;
18.1323;








